This month our definition of terms will look at regular and irregular features of size. Looking back we can see that a previous installment of our “definition of terms” looked at “features and features of size” which discussed features of size as they relate to parts and our larger scheme of geometric tolerancing.
This discussion will delve a little deeper into these features of size to differentiate between how these critters can be classified and used. There is a fairly wide variety of opinion about this in the GD&T user’s universe so I will try to enumerate some of the translations and practices we all use. First of all we should start with our ASME Y14.5’s definitions. A regular feature of size is said to be “one cylindrical or spherical surface (or circular element,) or two opposed parallel elements (or parallel surfaces,) associated with a directly toleranced dimension.” Now we need to consider another term that affects the results of our discussion and that is “size.” Both the terms regular feature of size and irregular features of size actually depend on how the word “size” is defined. This is fairly straightforward.
The vast majority of users accept that this identifies internal and external cylinders, planar thicknesses, and certain forms that have opposed parallel elements or surfaces, which all have a directly associated size dimension. Now before we go any further with this let’s look at our standard’s definition of an “irregular feature of size,” which is defined as two types: Type (a) “a directly toleranced feature or collection of features that contain or may be contained by an actual mating envelope that is a sphere, cylinder or pair of parallel planes.” Type (b) “a directly toleranced feature or collection of features that may contain or be contained in an actual mating envelope other than a sphere, cylinder or pair of parallel planes.” As we said earlier this is also fairly straightforward. By the words in this definition irregular features of size include those that are not spheres, cylinders or parallel planes, that are either internal or external features that can be contained by an actual mating envelope.
By now many people get rightfully weary of all the words, and I care about that but can do little to simplify the discussion because I study this stuff a lot and what is and is not acceptable hinges on these definitions. And the truth is many people agree that the Y14.5 standard has gaps in how things are defined and can be translated. I suppose if everything in the standard was clear and everyone agreed on its contents they wouldn’t need new updates. So here we might stop discussing words for a bit and look at some pictures that are worth a thousand words. The following graphics show examples of what most people accept to be regular and irregular features of size.
Regular features of size
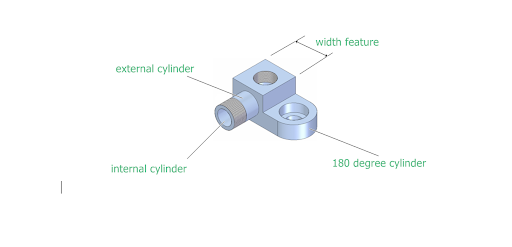
Irregular features of size, type A

Irregular FOS Type B

 Now let’s go back to our Y14.5 definitions: #1 is a direct quote from the standard under Regular feature of size, whereas #2 is a direct quote, again from the Y14.5 standard for irregular features of size.
Now let’s go back to our Y14.5 definitions: #1 is a direct quote from the standard under Regular feature of size, whereas #2 is a direct quote, again from the Y14.5 standard for irregular features of size.
- “one cylindrical or spherical surface (or circular element,) or two opposed parallel elements (or parallel surfaces,) associated with a directly toleranced dimension.”
- “a directly toleranced feature or collection of features that contain or may be contained by an actual mating envelope that is a sphere, cylinder or pair of parallel planes.”
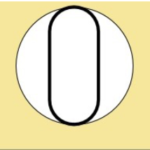
Looking at them this close together allows us to dissect their differences as concisely as possible to determine what the differences are between both number one’s and number two’s meanings. “Apparently there is only one difference, which is for regular features of size only one allowable directly toleranced cylindrical or spherical surface or element or two opposed parallel surfaces or elements. And for irregular features of size there can be one or a collection of directly toleranced cylindrical, spherical or parallel features of size.” Breaking this down even further we can say that there can only be one regular feature of size that fits the definition but there can be one or a collection of irregular features of size that conform to the definition. So going one step further is it true that regular and irregular features of size can be the same if there is only one of them but their definition separates when irregular feature of size become a collection? This seems wrong or at least ambiguous. Ambiguous meaning unclear or inexact because a choice between alternatives has not been made. If that’s true then let’s look at some examples of what people in our field call irregular features of size. Alex Krulikowski, in his Fundamentals of GD&T, says that an obround, such as the one below, fits the definition of an irregular feature of size. The two linear sides of this shape can be contained in a pair of parallel planes but that ignores the two half cylinders on either end of the feature. Is this OK?  This is where I start to get off the bus. The definition in the standard says “may be contained by an actual mating envelope.” Well let’s look at the graphic on the previous page that shows an obround slot inside a circle. Isn’t that the same thing as above where this irregular feature of size, which is a collection of features, no it’s not a collection of holes or squares, it’s 2 radii or half cylinders and 2 opposing elements or planes, is meant to be a viable feature of size. We can contain it by contracting a circle around it but the parallel elements or planes of its long sides are really not relative to the mating envelope, except that they are inside it.
This is where I start to get off the bus. The definition in the standard says “may be contained by an actual mating envelope.” Well let’s look at the graphic on the previous page that shows an obround slot inside a circle. Isn’t that the same thing as above where this irregular feature of size, which is a collection of features, no it’s not a collection of holes or squares, it’s 2 radii or half cylinders and 2 opposing elements or planes, is meant to be a viable feature of size. We can contain it by contracting a circle around it but the parallel elements or planes of its long sides are really not relative to the mating envelope, except that they are inside it. 
How about this collection of features?

Or this one?
 They can both be contained by the same mating envelope as the obround we discussed earlier. So where does that leave us? Back to the words of the definitions in the standard. Irregular type A can be contained by a mating envelope that is a sphere, cylinder or pair of parallel planes and B can be contained by a mating envelope other than a sphere, cylinder or pair of parallel planes. So what is an “other?” And if we think of a way to properly define “other” how can we agree on how it should fit the feature? Below we see two pentagons. If they are proper type B irregular features of size, they must be contained by a mating envelope that is other than a sphere, cylinder or pair of parallel planes.
They can both be contained by the same mating envelope as the obround we discussed earlier. So where does that leave us? Back to the words of the definitions in the standard. Irregular type A can be contained by a mating envelope that is a sphere, cylinder or pair of parallel planes and B can be contained by a mating envelope other than a sphere, cylinder or pair of parallel planes. So what is an “other?” And if we think of a way to properly define “other” how can we agree on how it should fit the feature? Below we see two pentagons. If they are proper type B irregular features of size, they must be contained by a mating envelope that is other than a sphere, cylinder or pair of parallel planes. 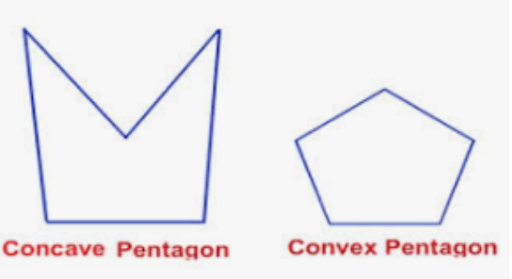 The concave example, if it can be, can be contained by a really weird shape of envelope. The convex example can be contained by an ellipse maybe? The first is not very conventional while the second is more conventional. Is this what the standards committee intended? I’ve spent more than a few hours Googling and looking for astute opinions on this subject because I teach GD&T and my students usually like static answers to the subjects we study. By static I mean ones that don’t wiggle around. So one thing I read about the subject of irregular features of size simply said Type A features are of a sort that can easily be constructed and then be contained in “envelopes that are spheres, cyl…yadda-yadda.” Things like triangles and symmetrical pentagons. While “type B irregular features of size” are everything else. I want to argue with this, but based on the definitions I can’t. The phrase “contained in other than a sphere, cylinder or pair of parallel planes” is succinct. If we accept that the word other rules the alternatives then other means every mating envelope that’s not a sphere, cylinder or pair of parallel planes, which includes all possible envelopes. So have we nailed it down? I can easily say No! There are going to be people who say that by the way they read the standard that some part of this is way off base. I’m hoping someone does because I don’t get a lot of response to the words I write for this blog and even words of disagreement will be welcome. The fact is that I think the wording in the standard leaves room for “wiggling.”
The concave example, if it can be, can be contained by a really weird shape of envelope. The convex example can be contained by an ellipse maybe? The first is not very conventional while the second is more conventional. Is this what the standards committee intended? I’ve spent more than a few hours Googling and looking for astute opinions on this subject because I teach GD&T and my students usually like static answers to the subjects we study. By static I mean ones that don’t wiggle around. So one thing I read about the subject of irregular features of size simply said Type A features are of a sort that can easily be constructed and then be contained in “envelopes that are spheres, cyl…yadda-yadda.” Things like triangles and symmetrical pentagons. While “type B irregular features of size” are everything else. I want to argue with this, but based on the definitions I can’t. The phrase “contained in other than a sphere, cylinder or pair of parallel planes” is succinct. If we accept that the word other rules the alternatives then other means every mating envelope that’s not a sphere, cylinder or pair of parallel planes, which includes all possible envelopes. So have we nailed it down? I can easily say No! There are going to be people who say that by the way they read the standard that some part of this is way off base. I’m hoping someone does because I don’t get a lot of response to the words I write for this blog and even words of disagreement will be welcome. The fact is that I think the wording in the standard leaves room for “wiggling.”
I’ll close with a comment I read last week made by an ASME “Senior Certified” member of our GD&T community of users. He said that he passed the Senior level exam on the first try, with only one mistake. Words with which he meant to impress, and I was. He was recommending that prospective aspirants to the Senior Certification process study the ASME Standard not the vast array of engineers and specialists that give their opinions of what the standard says. I can’t argue with that other than to say I consider myself to be well educated. I write a lot. I teach 6 college subjects at a specialized community college manufacturing program. I’ve written 3 novels. I work a full time job as a manufacturing engineer and mechanical parts and assemblies estimator. I know this sounds like a buildup to “you should listen to me because.” But it’s not. I have and use my well worn and dogeared copies of the 1982, 1994 and 2009 Y14.5 standards and one thing is abundantly clear to me. I have to read nearly every paragraph in them at least three or four times and often over a period of days to confidently digest what they say. I have to pour over diagrams and examples and I often copy a paragraph on page 34 and tape it beside one on page 284 so I can compare what they’re saying. And following that I spend time wondering if I really understand what I’ve translated. So I’ll close with a thank you sent out to all the brave members of the standards committee and all the people out there that work hard to promote the adoption of this system we all use. These thoughts are my interpretation of the subjects discussed and I’ll bet I end up with more than a few new perspectives on them in the future.








One thing that should get more attention in this discussion is the definition of an Actual Mating Envelope, as this term is also part of the definition of both types of irregular features of size.
Is a cylindrical envelope containing a triangular or pentagonal feature contacting only the corners like in the posted examples conforms to the definition of an actual mating envelope for those features? If yes, both can be valid as irregular features of size type A, can’t they? Or maybe a triangular or pentagonal counterpart envelope that makes maximum possible contact with the flat surfaces is a better representation of an actual mating envelope per the standard definitions? Maybe the decision between type A and type B also depends on how the feature was dimensioned, and not only on its shape?